ICLR2020部分NAS投稿论文解读
1.stabilizing DARTS with Amended grarident estimation on architectural parameters
将darts的loss分为两个部分,对第二个部分进行了推证,提出了新的一种数学形式去近似这个loss,并进行了solid的数学证明。
\[\begin{equation} \mathbf{g}_{2}^{\prime}=-\left.\left.\eta \cdot \nabla_{\boldsymbol{\alpha}, \boldsymbol{\omega}}^{2} \mathcal{L}_{\text {train }}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\omega=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \cdot \mathbf{H} \cdot \nabla_{\boldsymbol{\omega}} \mathcal{L}_{\text {val }}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\boldsymbol{\omega}=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \end{equation}\]
提出DARTS的二阶偏导的更合理的近似,下面这个公式,第一个部分称为\(g_1\),通过梯度的反向传播得到。第二部分称为\(g_2\),更合理的近似为\(g_2'\)。 \[ \begin{aligned} \nabla_{\boldsymbol{\alpha}} \mathcal{L}_{\mathrm{val}}\left(\boldsymbol{\omega}^{\star}(\boldsymbol{\alpha}), \boldsymbol{\alpha}\right)|_{\boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} =& \nabla_{\boldsymbol{\alpha}} \mathcal{L}_{\mathrm{val}}(\boldsymbol{\omega}, \boldsymbol{\alpha})|_{\boldsymbol{\omega}=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} - \\ & \nabla_{\boldsymbol{\alpha}, \boldsymbol{\omega}}^{2} \mathcal{L}_{\mathrm{train}}(\boldsymbol{\omega}, \boldsymbol{\alpha})|_{\omega=\boldsymbol{\omega}^{*} \left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \cdot \mathbf{H}^{-1} \cdot \nabla_{\boldsymbol{\omega}} \mathcal{L}_{\mathrm{val}}(\boldsymbol{\omega}, \boldsymbol{\alpha})|_{\omega=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \end{aligned} \] \[ \begin{aligned} \left\langle\mathbf{g}_{2}^{\prime}, \mathbf{g}_{2}\right\rangle=&\left.\left.\eta \cdot \nabla_{\omega} \mathcal{L}_{\mathrm{val}}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\omega=\omega^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} ^{\top} \cdot \mathbf{H}^{-1} \cdot \nabla_{\boldsymbol{\omega}, \boldsymbol{\alpha}}^{2} \mathcal{L}_{\mathrm{train}}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\omega=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \\ &\left.\left.\nabla_{\boldsymbol{\alpha}, \boldsymbol{\omega}}^{2} \mathcal{L}_{\mathrm{train}}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\omega=\boldsymbol{\omega}^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \cdot \mathbf{H} \cdot \nabla_{\boldsymbol{\omega}} \mathcal{L}_{\mathrm{val}}(\boldsymbol{\omega}, \boldsymbol{\alpha})\right|_{\omega=\omega^{*}\left(\boldsymbol{\alpha}_{t}\right), \boldsymbol{\alpha}=\boldsymbol{\alpha}_{t}} \end{aligned} \] 并证明\(g_2'\)与\(g_2\)的乘积恒大于0,也就是夹角小于90度。
2. DARTS+: Improved Differentiable Architecture Search with Early Stopping
随着epoch数量的增多,DARTS倾向于skip-connection,造成模型的表现下降
提出一种提前停止训练的标准,让模型搜索提前停止。
- 当模型中出现两个skip-connection的时候
- 当模型中的\(\alpha\)参数的排列顺序不再发生改变的时候(\(\alpha\)的值是各个Primitives的概率)
3. PC-DARTS
uses partial- channel connections to reduce search time,
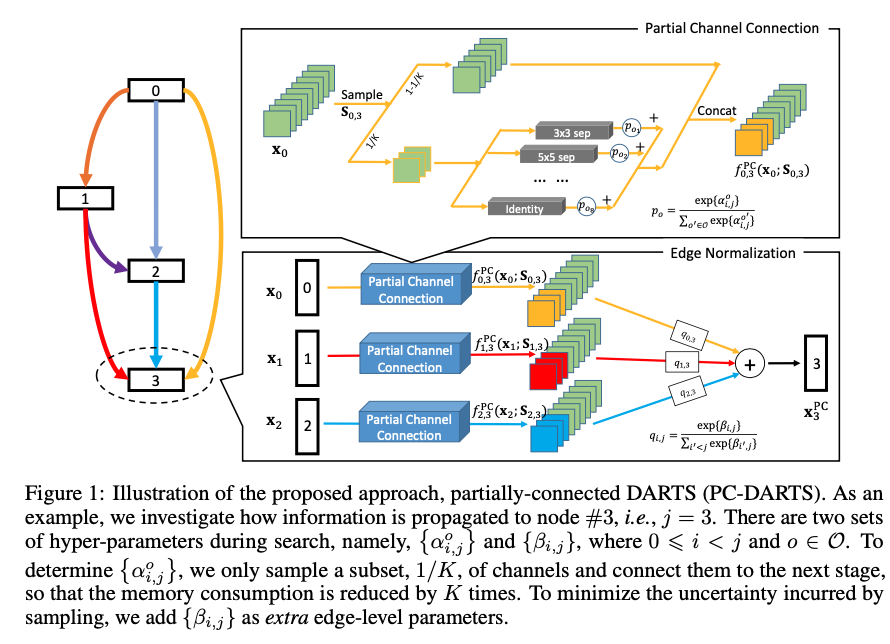
Partial Channel Connections
只将1/K 的channels使用primitives连接,其余的channels选择直接连接,也就是,从\(node_i\)到\(node_j\)的边中,选出一部分channel使用非identity的方式连接,其余的使用identity,经过非identity方式的channel乘以softmax以后的\(\alpha\)权重相加,再和原来的channel一起concat。这样做的处理,是希望占用的内存更小,使用更大的batch_size,提升训练和模型表现。
削弱了weight-free操作的影响。
Edge Normalization
\(node_i\)前面所有的\(node\)都需要输出到它,设计权重\(\beta\),乘以这些边,得到\(node_i\)的值。
4. P-DARTS
将layer的数目慢慢增加。
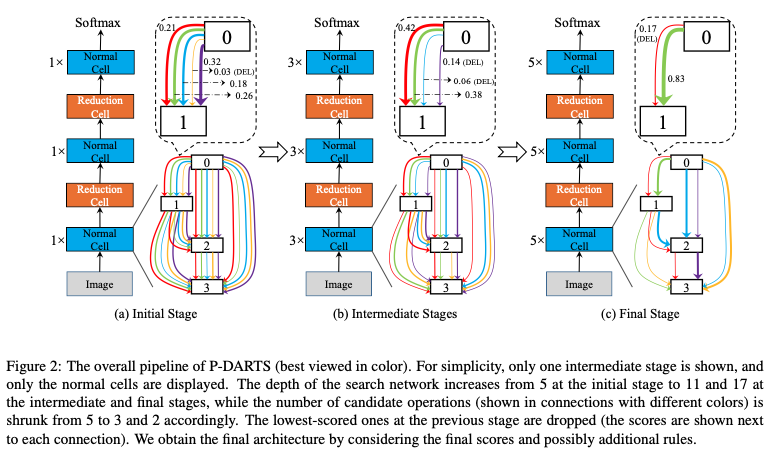
- searching for 25 epochs instead of 50 epochs,
- adopting dropout after skip-connects
- manually reducing the number of skip-connects to two
修剪skip-connection的数目操作只能发生在第一个
5. Searching for A Robust Neural Architecture in Four GPU Hours
每次只计算最大权重的梯度,只BP最大权重的梯度,以此来减少计算量和GPU显存。
6. ProxylessNAS
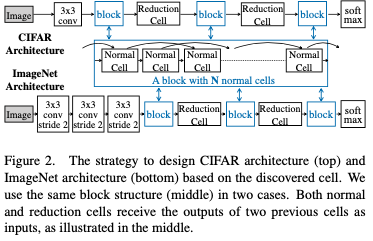
ProxylessNAS 不同于以前的在代理数据集上面进行搜索以后转移到大数据集类似ImageNet上面进行训练测试,而是直接在大数据集上面进行搜索,它的搜素的算子数目被大大减少以减小搜索的空间,降低搜索的难度。
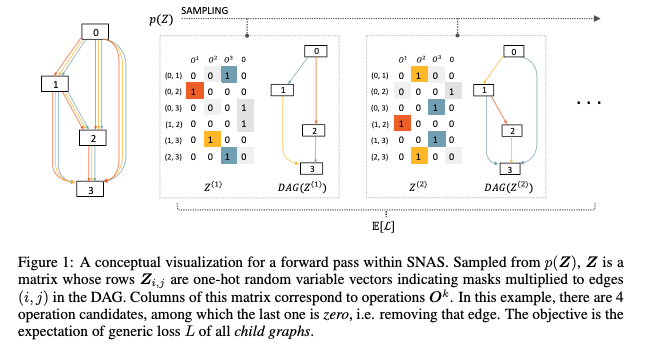
7. SNAS
SNAS故事讲的不一样,但是本质上来说,跟DARTS基本一样的原理,即使用operation的加权和来代替单独的operation。 它使用了gumble-softmax trick,使用概率采样出的权值而不是固定的权值来计算加权和,同时增加temperature,使得采样出的权值更加接近one-hot的权值,来拟合单独的operation。
SNAS论文里面证明了,使用这种方式采样进行优化的过程,近似等价于强化学习采样网络学习进行优化的过程